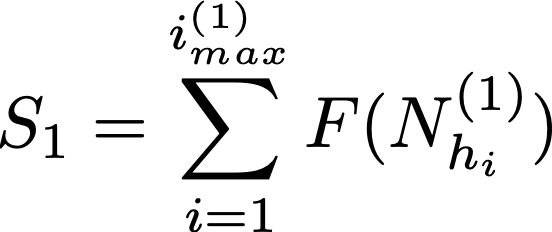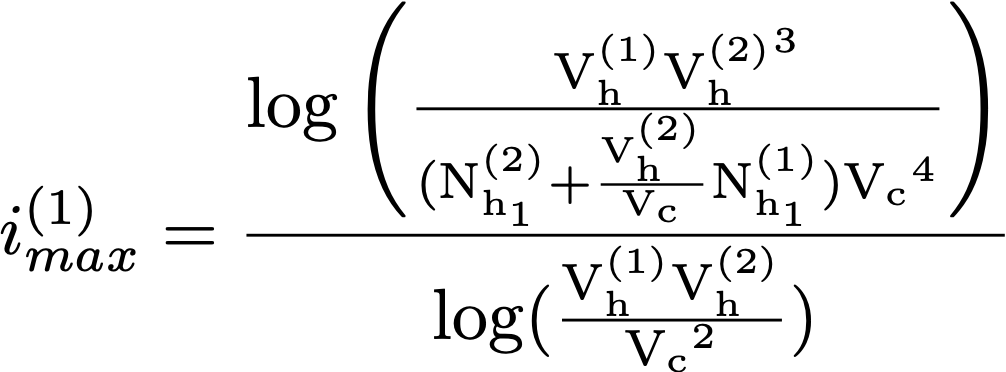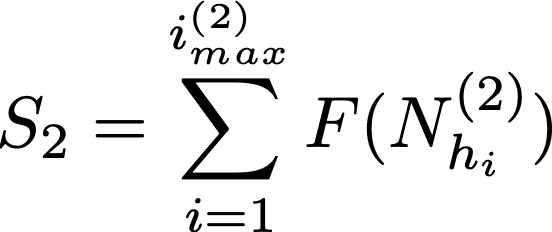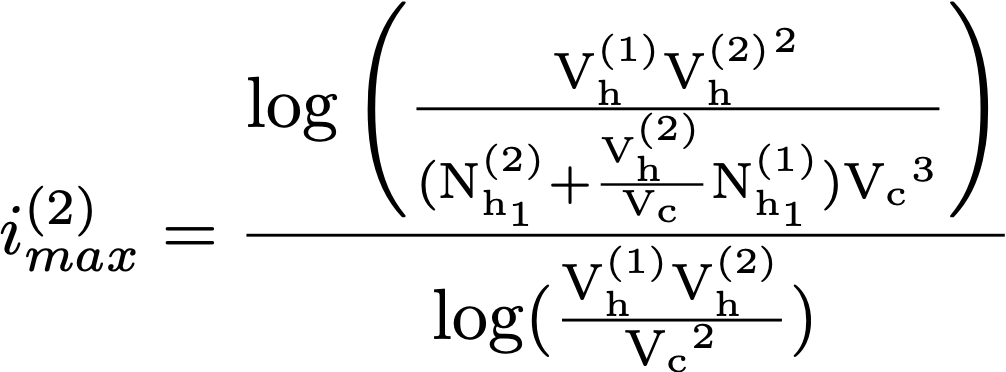Formules de construction de chaîne : Différence entre versions
(→Formule de calcul de la taille des chaînes principales) |
|||
| (6 révisions intermédiaires par un utilisateur sont masquées) | |||
| Ligne 3 : | Ligne 3 : | ||
Cette page aura pour but de détailler les formules (et leurs démonstrations) permettant de prédire le résultat, en terme de dommages envoyés, d'un échange de chaînes principales entre deux joueurs qui reconstruisent pendant que la chaîne adverse se résoud, en fonction de la vitesse de construction de chaque joueur et des paramètres du jeu. | Cette page aura pour but de détailler les formules (et leurs démonstrations) permettant de prédire le résultat, en terme de dommages envoyés, d'un échange de chaînes principales entre deux joueurs qui reconstruisent pendant que la chaîne adverse se résoud, en fonction de la vitesse de construction de chaque joueur et des paramètres du jeu. | ||
| − | ==Notations | + | '''Les formules dans cette page sont à améliorer : des fois dans la démonstration, il faut prendre la partie entière du nombre de hits, des fois non.''' |
| + | |||
| + | ==Notations, conventions et hypothèses== | ||
Dans les quantités présentées, les deux joueurs sont référencés par un indice i valant 1 ou 2. Le joueur 1 est celui qui initie l'échange de chaînes principales. | Dans les quantités présentées, les deux joueurs sont référencés par un indice i valant 1 ou 2. Le joueur 1 est celui qui initie l'échange de chaînes principales. | ||
On note : | On note : | ||
| Ligne 11 : | Ligne 13 : | ||
* H le nombre de hits construits par paire posée, en hits par paire, | * H le nombre de hits construits par paire posée, en hits par paire, | ||
* V<sub>h</sub><sup>(i)</sup> = H * V<sub>p</sub><sup>(i)</sup>, la vitesse de construction du joueur i, en hits par seconde. | * V<sub>h</sub><sup>(i)</sup> = H * V<sub>p</sub><sup>(i)</sup>, la vitesse de construction du joueur i, en hits par seconde. | ||
| + | |||
| + | Notons que la vitesse de construction d'un joueur, en hits par seconde, est en réalité dépendante d'énormément de paramètres, comme le niveau de fatigue et de concentration du joueur qui peuvent varier au cours du point en cours et au cours du match entier. Cependant, si on considère le joueur comme suffisamment constant, alors on peut estimer que sa vitesse de construction dépend uniquement du nombre de hits actuel dans sa chaîne. En effet, les joueurs sont en pratique souvent plus rapide à construire leur base que leur étage, et des caps comme le second virage, donc aux alentours du dépassement du 12ème hit, peuvent être plus longs à passer que les hits d'avant et après. Il est donc raisonnable que la courbe de la vitesse de construction en fonction du nombre de hits dans la chaîne est non-linéaire et non-monotone. Si on n'est pas en mesure de calculer dans le détail cette vitesse pour un adversaire qu'on étudie, il est simplement possible de calculer une vitesse moyenne de construction, qui approchera les résultats plus ou moins correctement la réalité. Pour ce faire, il faut garder une trace du temps que met le joueur à construire un grand nombre de chaînes de différentes longueurs, diviser à chaque fois le temps écoulé par le nombre de hits atteint et faire la moyenne des résultats obtenus. | ||
| + | |||
| + | L'hypothèse est faite que les chaînes construites comportent 4 puyos à chacun de leurs hits, afin de regarder le cas où la montée en hits est la plus rapide. | ||
==Schéma type d'un échange de chaînes principales== | ==Schéma type d'un échange de chaînes principales== | ||
| Ligne 28 : | Ligne 34 : | ||
et enfin, pour i > 2 | et enfin, pour i > 2 | ||
| − | [[Fichier: | + | [[Fichier:Nhi1_2.png|300px|centré]] |
et pour i > 1 | et pour i > 1 | ||
| − | [[Fichier: | + | [[Fichier:Nhi2_2.png|300px|centré]] |
===Simplifications=== | ===Simplifications=== | ||
| Ligne 49 : | Ligne 55 : | ||
===Exemples pratiques=== | ===Exemples pratiques=== | ||
| + | |||
| + | ==Eléments de probabilités associées== | ||
| + | |||
| + | Les formules données plus haut permettent de trouver à quoi peut ressembler l'échange le plus long possible. On peut associer à chaque étape une probabilité de réussite (probabilité que le joueur dont c'est le tour obtienne un de ses starters à temps), et ainsi déterminer les chances qu'un échange dure plus ou moins longtemps dans des conditions optimales de construction. Cela peut servir à déterminer l'espérance de gain d'un envoi de chaîne principale, ou d'une attaque rapide provoquant l'envoi de la chaîne principale adverse. | ||
==Formule de calcul du score résultant d'un échange== | ==Formule de calcul du score résultant d'un échange== | ||
| + | |||
| + | Soit F(N) la fonction qui associe à une chaîne de N hits un score, qui représente directement les dommages envoyés par la chaîne. On considère le cas où le nombre de puyos par hit est de 4 et qu'il n'y a donc ni bonus de couleurs ni bonus de groupes. Cette fonction peut s'écrire sous la forme | ||
| + | * F(1) = 40 | ||
| + | * F(2) = 320, F(3) = 640 | ||
| + | * F(N) = 1280 * N - 3840, pour N > 3 | ||
| + | |||
| + | Si on note S1 le score obtenu sur le total de l'échange par le joueur 1, et S2 le score obtenu sur le total de l'échange par le joueur 2, on a | ||
| + | |||
| + | [[Fichier:S1.png|150px|centré]] | ||
| + | |||
| + | avec | ||
| + | |||
| + | [[Fichier:Imax1.png|250px|centré]] | ||
| + | |||
| + | et on a | ||
| + | |||
| + | [[Fichier:S2.png|150px|centré]] | ||
| + | |||
| + | avec | ||
| + | |||
| + | [[Fichier:Imax2.png|250px|centré]] | ||
| + | |||
| + | Les i<sub>max</sub> correspondent à l'indice où la chaîne du joueur ne fait plus que 1 hit, et donc l'indice maximal qu'il est nécessaire de considérer pour le score. Le logarithme utilisé ici est le logarithme naturel (ou népérien). | ||
| + | Il est important de remarquer que pour utiliser ces 4 formules, il faut arrondir à l'entier inférieur les valeurs de i<sub>max</sub> et les valeurs des nombres de hits dans la chaîne, calculés par les formules de la section précédente, quand on les injecte dans la formule de score S1 ou S2. | ||
[[Catégorie:Articles]] | [[Catégorie:Articles]] | ||
Version actuelle en date du 21 février 2020 à 09:24
Cette page est en cours d'élaboration !
Cette page aura pour but de détailler les formules (et leurs démonstrations) permettant de prédire le résultat, en terme de dommages envoyés, d'un échange de chaînes principales entre deux joueurs qui reconstruisent pendant que la chaîne adverse se résoud, en fonction de la vitesse de construction de chaque joueur et des paramètres du jeu.
Les formules dans cette page sont à améliorer : des fois dans la démonstration, il faut prendre la partie entière du nombre de hits, des fois non.
Sommaire
Notations, conventions et hypothèses
Dans les quantités présentées, les deux joueurs sont référencés par un indice i valant 1 ou 2. Le joueur 1 est celui qui initie l'échange de chaînes principales. On note :
- Vp(i) la vitesse de posage du joueur i, en paires par seconde,
- Vc la vitesse de cassage d'une chaîne, en hits par seconde,
- tc le temps de cassage d'une chaîne, en secondes,
- H le nombre de hits construits par paire posée, en hits par paire,
- Vh(i) = H * Vp(i), la vitesse de construction du joueur i, en hits par seconde.
Notons que la vitesse de construction d'un joueur, en hits par seconde, est en réalité dépendante d'énormément de paramètres, comme le niveau de fatigue et de concentration du joueur qui peuvent varier au cours du point en cours et au cours du match entier. Cependant, si on considère le joueur comme suffisamment constant, alors on peut estimer que sa vitesse de construction dépend uniquement du nombre de hits actuel dans sa chaîne. En effet, les joueurs sont en pratique souvent plus rapide à construire leur base que leur étage, et des caps comme le second virage, donc aux alentours du dépassement du 12ème hit, peuvent être plus longs à passer que les hits d'avant et après. Il est donc raisonnable que la courbe de la vitesse de construction en fonction du nombre de hits dans la chaîne est non-linéaire et non-monotone. Si on n'est pas en mesure de calculer dans le détail cette vitesse pour un adversaire qu'on étudie, il est simplement possible de calculer une vitesse moyenne de construction, qui approchera les résultats plus ou moins correctement la réalité. Pour ce faire, il faut garder une trace du temps que met le joueur à construire un grand nombre de chaînes de différentes longueurs, diviser à chaque fois le temps écoulé par le nombre de hits atteint et faire la moyenne des résultats obtenus.
L'hypothèse est faite que les chaînes construites comportent 4 puyos à chacun de leurs hits, afin de regarder le cas où la montée en hits est la plus rapide.
Schéma type d'un échange de chaînes principales
Formule de calcul de la taille des chaînes principales
On considère, comme dans le schéma type présenté au-dessus, que la séquence d'échange se passe au tour par tour, chaque tour donnant l'occasion à un joueur de répondre à la chaîne de l'autre.
Soient Nhj(1) et Nhj(2) le nombre de hits dans les chaînes principales des joueurs 1 et 2 à l'instant j. j = 1 correspond au début de l'échange, initié par le joueur 1.
Cas général
On a
et enfin, pour i > 2
et pour i > 1
Simplifications
Si on fait l'hypothèse que les deux joueurs construisent exactement à la même vitesse, alors on a Vh<\sub>(1) = Vh<\sub>(2) et les formules deviennent
puis, pour i > 2
et pour i > 1
Exemples pratiques
Eléments de probabilités associées
Les formules données plus haut permettent de trouver à quoi peut ressembler l'échange le plus long possible. On peut associer à chaque étape une probabilité de réussite (probabilité que le joueur dont c'est le tour obtienne un de ses starters à temps), et ainsi déterminer les chances qu'un échange dure plus ou moins longtemps dans des conditions optimales de construction. Cela peut servir à déterminer l'espérance de gain d'un envoi de chaîne principale, ou d'une attaque rapide provoquant l'envoi de la chaîne principale adverse.
Formule de calcul du score résultant d'un échange
Soit F(N) la fonction qui associe à une chaîne de N hits un score, qui représente directement les dommages envoyés par la chaîne. On considère le cas où le nombre de puyos par hit est de 4 et qu'il n'y a donc ni bonus de couleurs ni bonus de groupes. Cette fonction peut s'écrire sous la forme
- F(1) = 40
- F(2) = 320, F(3) = 640
- F(N) = 1280 * N - 3840, pour N > 3
Si on note S1 le score obtenu sur le total de l'échange par le joueur 1, et S2 le score obtenu sur le total de l'échange par le joueur 2, on a
avec
et on a
avec
Les imax correspondent à l'indice où la chaîne du joueur ne fait plus que 1 hit, et donc l'indice maximal qu'il est nécessaire de considérer pour le score. Le logarithme utilisé ici est le logarithme naturel (ou népérien). Il est important de remarquer que pour utiliser ces 4 formules, il faut arrondir à l'entier inférieur les valeurs de imax et les valeurs des nombres de hits dans la chaîne, calculés par les formules de la section précédente, quand on les injecte dans la formule de score S1 ou S2.